「毎月◯万円の返済なら、いくらまで借りられる?」
──そんな疑問をシミュレーションできるのが PV関数 です。
PV関数は、ローンの返済額・返済期間・金利(利率)から、借り入れ可能な金額(現在価値) を求める関数です。
この記事では、PV関数の使い方をわかりやすく解説します。
PV関数とは?
PV関数は、「将来の支払や収入の流れを、今の価値に直して考える関数」です。
ローン計算では、毎月の支払額(PMT)、利率(RATE)、返済期間(NPER)をもとに、
現時点で借りられる元金(PV)=借入可能額 を計算します。
書式
=PV(利率, 期間, 定期支払額, [将来価値], [支払期日])
引数の説明
- 利率:利率を指定します。
年利を月単位に変える場合は「年利 ÷ 12」。 - 期間:支払回数を指定します。
ローン期間が10年で毎月払いなら「10×12=120」。 - 定期支払額:毎月の返済額を指定します。
支出なのでマイナスの値で入力します。 - 将来価値(省略可):将来価値。完済後に残す金額(通常は0)。
- 支払期日(省略可):支払タイミング。期末払い=0(既定値)、期首払い=1。
使用例
例:毎月5万円を10年間返済できる場合の借入可能額を求める
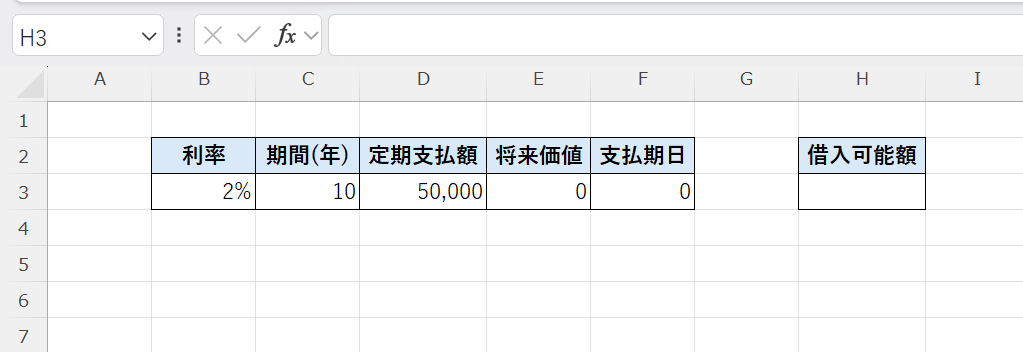
ここでは、年利2.4%で毎月5万円を10年間返済する場合の、借り入れ可能額をPV関数を使って求めてみましょう。
セルH3に次の式を入力します👇
=-PV(B3/12,C3*12,D3,E3,F3)
この式は、
- 利率:月利0.2%(年利2.4%)
- 期間:120回(10年間)
- 定期支払額:5万円
という条件での借入可能額(現在価値)を求めます。
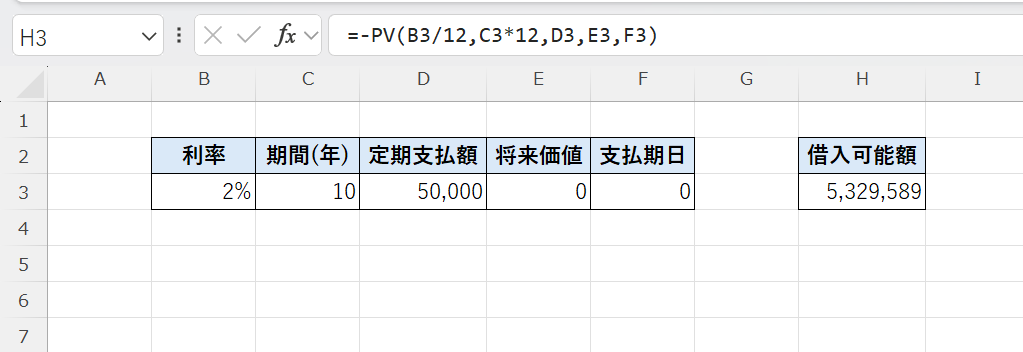
計算結果は 約5,329,589円(約533万円) になります。
つまり、年利2.4%で毎月5万円を10年間返済できるなら、借り入れ可能額は約471万円となります。
活用例
- 住宅ローンの試算:年収や毎月返済額から購入可能な物件価格を逆算。
- 自動車ローンの比較:金利ごとの借入可能額を比較して選択。
- 教育ローンや奨学金の検討:期間・金利・返済額を基に借入限度を算出。
- 家計シミュレーション:返済負担率を踏まえて無理のない借入額を確認。
注意点
- 返済額(pmt)はマイナスで入力
支出を意味するため、符号が逆だと結果も反転します。 - 金利(rate)は期間に合わせる
年利をそのまま入れると誤差が出るため、月利換算が必要です。 - 返済回数(nper)は年×12などで指定
期間を月単位で正しく設定しましょう。 - 結果がマイナスで出る理由
Excelでは支出(返済)をマイナス、入金(借入)をプラスとして計算しているためです。
関連関数
| 関数名 | 内容 |
|---|---|
| PMT関数 | 毎回の返済額を求める |
| FV関数 | 将来の残高(将来価値)を求める |
| NPER関数 | 完済までの回数を求める |
| RATE関数 | 利率を求める |
| NPV関数 | 投資の現在価値(複数キャッシュフロー)を求める |
まとめ
PV関数は、ローンの借入可能額(今借りられる元金)を求めるのに最適な関数です。
返済額・期間・金利の3つを入力するだけで、「自分はいくらまで借りられるのか」をすぐに試算できます。
住宅ローン、車のローン、教育費など、大きな支出を計画するときに「無理のない返済額」を確認するための必須ツールです。

