「毎年の利率が違う場合、5年後の金額はいくらになるの?」
そんなときに便利なのが FVSCHEDULE関数 です。
FVSCHEDULE関数は、複数の期間ごとに異なる利率が設定されている場合に、
元本が将来いくらになるか(将来価値)を簡単に求められる関数です。
定期預金や投資シミュレーションなどで活用できます。
🧮 FVSCHEDULE関数とは?
FVSCHEDULE関数は、元金と複数の利率をもとに、
最終的な将来価値(Future Value)を計算する関数です。
複利計算を年ごとに個別利率で行えるため、
毎年の金利が変動するような現実的なシナリオに対応できます。
書式
=FVSCHEDULE(元金, 利率配列)
引数の説明
- 元金:初期の金額(現在の投資額や預金額)
- 利率の配列:各期間(年や月)ごとの利率をまとめた範囲または配列
使用例
例:5年間の利率が異なる場合の将来価値を求める
元金(初期投資額):100,000円
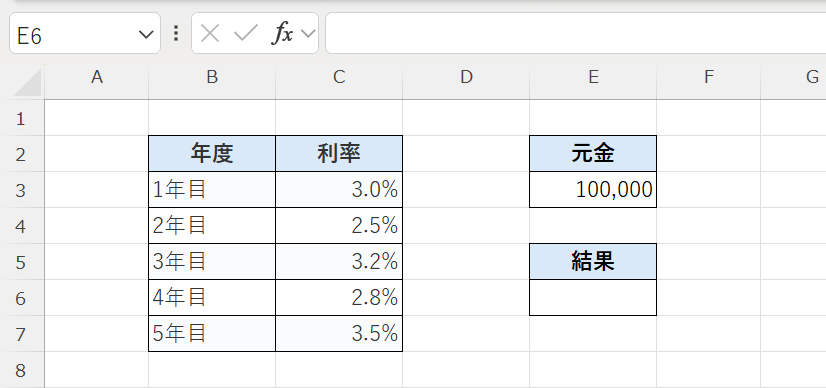
=FVSCHEDULE(E3,C3:C7)
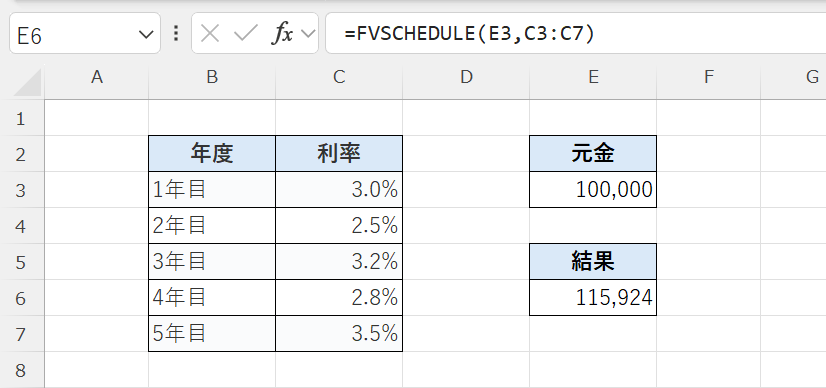
結果:約115,924円
この結果は、元金10万円を、
毎年異なる利率(3%、2.5%、3.2%、2.8%、3.5%)で5年間運用した場合の将来価値です。
各年の計算は次のようになります👇
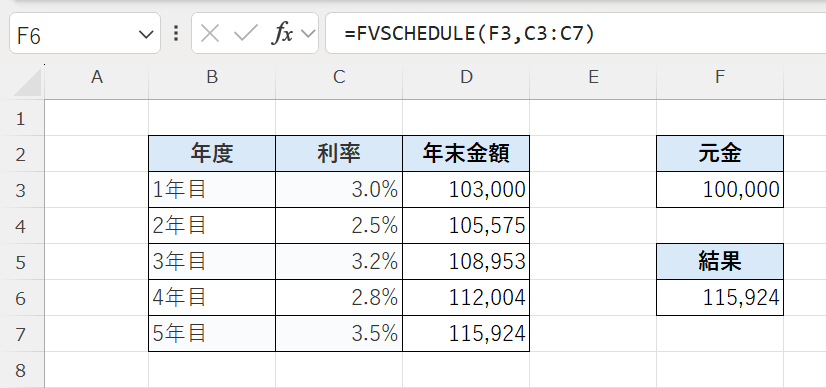
つまり、5年間で約15,924円の増加となります。
FVSCHEDULE関数は、年ごとの金利変動を反映した、より現実的な複利計算が可能です。
注意点
- 負の利率(マイナス成長)を含めることも可能です。
関連関数
まとめ
FVSCHEDULE関数は、毎年の利率が異なる複利計算を簡単に行える便利な関数です。
一定利率しか扱えないFV関数に比べて、現実の投資や預金の変動をより正確にシミュレーションできます。

