データのばらつき具合を知りたいときに役立つのが 分散 です。
Excelでは、データ全体(母集団)をもとに分散を求める場合に VAR.P関数 を使います。
※VAR.P関数は旧形式のVARP関数の後継であり、Excel 2010以降では VAR.P関数 が標準として推奨されています。
VAR.P関数とは?
VAR.P関数 は、指定した範囲を母集団(全体)とみなして、データのばらつきを示す母分散を求める関数です。
データ全体を分析するときや、すべての値を対象にばらつきを知りたいときに使用します。
分散とは?
分散とは、データのばらつきの大きさを表す指標です。
データ全体が平均値からどのくらい離れているかを、数値で示します。
たとえば、同じ平均点が80点でも、
- 点数が「78~82点」に集中していれば → 分散は小さい(ばらつきが少ない)
- 点数が「60~100点」と幅が広ければ → 分散は大きい(ばらつきが大きい)
というように、数値が大きいほどデータのばらつきが大きいことを意味します。
書式
=VAR.P(数値1, [数値2], …)
引数の説明
- 数値1, [数値2], …:分散を求めたい数値または範囲。
使用例(テストの点数で母分散を求める)
次の表は、12人のテスト結果です。
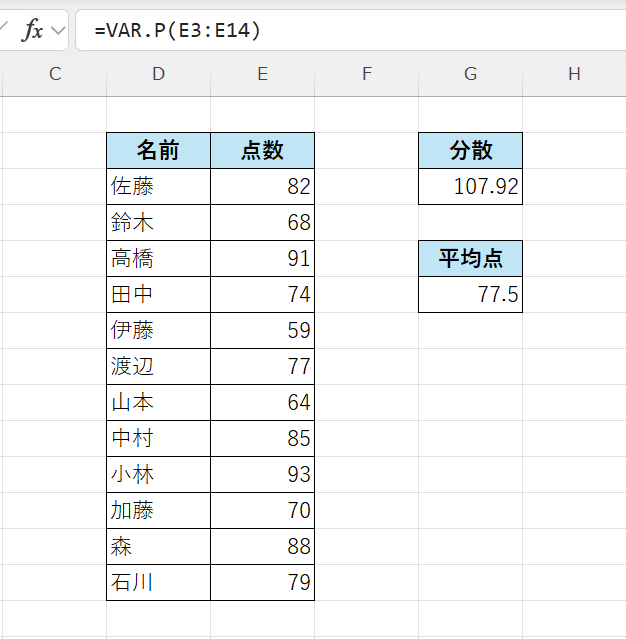
このとき、点数の分散(データ全体のばらつき)を求めるには次のように入力します。
=VAR.P(E3:E14)
👉 結果:およそ 107.92
この値は、12人全員を母集団として見た場合の「母分散」です。
平均値(約77.5点)からどれくらい点数が離れているかを示しています。
結果をどう見るか
先ほどのテスト12人のデータで求めた分散は「107.92」でした。
この数値をどう見るかというと、
- 各生徒の点数は平均(約77.5点)から
平均して「√107.9 ≒ 10.4点」ほど離れている - つまり、ほとんどの人は 平均±10点(約67〜87点) の範囲に集中しているという解釈になります。
💡 分散の平方根(√分散)が「標準偏差」です。
標準偏差が10点なら、「±10点の範囲に多くのデータがある」と理解しやすくなります。
活用例
- クラスのテスト結果のばらつきを分析
- 社員評価や売上データの安定性を確認
- 製品検査や品質データの一貫性の評価
- 分析データの変動の大きさを可視化
注意点
| 注意点 | 内容 |
|---|---|
| 母集団を対象とする | すべてのデータを含むときに使用。標本データの場合は VAR.S を使う。 |
| 結果の単位 | 元データの単位を二乗した値(例:点数²)になる。標準偏差を求めたい場合は STDEV.P を使う。 |
| 範囲指定 | 空白セルや文字列は自動的に無視される。 |
| 旧関数との違い | VARP は旧バージョン。現在は VAR.P の使用が推奨。 |
関連関数
| 関数 | 説明 |
|---|---|
| VAR.S | 標本(サンプル)を対象とした分散を求める |
| STDEV.P | 母集団を対象とした標準偏差を求める |
| STDEV.S | 標本を対象とした標準偏差を求める |
| AVERAGE | 平均値を求める(分散計算の基礎) |
まとめ
VAR.P関数 は、データ全体を母集団とみなして母分散(全体のばらつき)を求める関数です。
テスト結果や品質データなどの安定性を評価したいときに便利で、Excel 2010以降ではVARPの代わりにVAR.Pを使うのが基本です。
標準偏差を求める際は STDEV.P 関数と組み合わせると、より直感的にデータの傾向をつかめます。
