「気温が上がるとアイスクリームの売上が増える」──その関係性をデータから読み取りたいと思ったことはありませんか?
TREND関数を使えば、データの傾向をもとに将来の数値を予測する「重回帰分析(じゅうかいきぶんせき)」をとても簡単に行うことができます。
複雑な統計知識がなくても、Excelの関数だけで「傾向の把握」や「予測値の計算」ができるのが特徴です。この記事では、TREND関数を使った重回帰分析の方法をわかりやすく解説します。
TREND関数とは?
TREND関数は、既知のデータ(XとY)の関係をもとに、
その傾向を表す「回帰直線」を求め、未知のX値に対するY値を予測する関数です。
Excelでは、統計学でいう「単回帰分析」や「重回帰分析」を関数で簡単に実行できます。
複数の説明変数を指定することで、気温や広告費など複数要因を考慮した予測(重回帰分析)も可能です。
重回帰分析とは?
「気温が高いほどアイスが売れる」──これは、1つの要因(気温)が結果(売上)に影響している関係ですね。このように、1つの原因から結果を予測するのを「回帰分析(かいきぶんせき)」といいます。
しかし、現実の世界では「気温」だけでなく、たとえば「曜日(休日 or 平日)」「天気は晴れか雨か」といったいくつもの要因が同時に影響します。
そこで登場するのが 重回帰分析 です。
重回帰分析とは、「複数の原因(説明変数)」から「1つの結果(目的変数)」を予測する方法のことです。
たとえば、アイスクリームの売上を予測したいときに、「気温」、「曜日(休日 or 平日)」、「天気」などをまとめて使って予測する──これが重回帰分析です。
書式
=TREND(既知のy, 既知のx, [新しいx], [定数])
引数の説明
- 既知のy:既知のY値(目的変数)を指定します。
たとえば売上や成績、アクセス数など、予測したい数値です。 - 既知のx:既知のX値(説明変数)を指定します。
気温、広告費、日付など、Yに影響を与える要素です。 - 新しいx:予測したいX値を指定します。
将来の条件や新しいデータを入力して予測します。 - 定数:切片を含めるかどうかを指定します。
通常は「TRUE」または省略でOK(切片を自動で計算)。
TREND関数の使い方
例:気温・天気・曜日からアイスクリームの売上を予測する
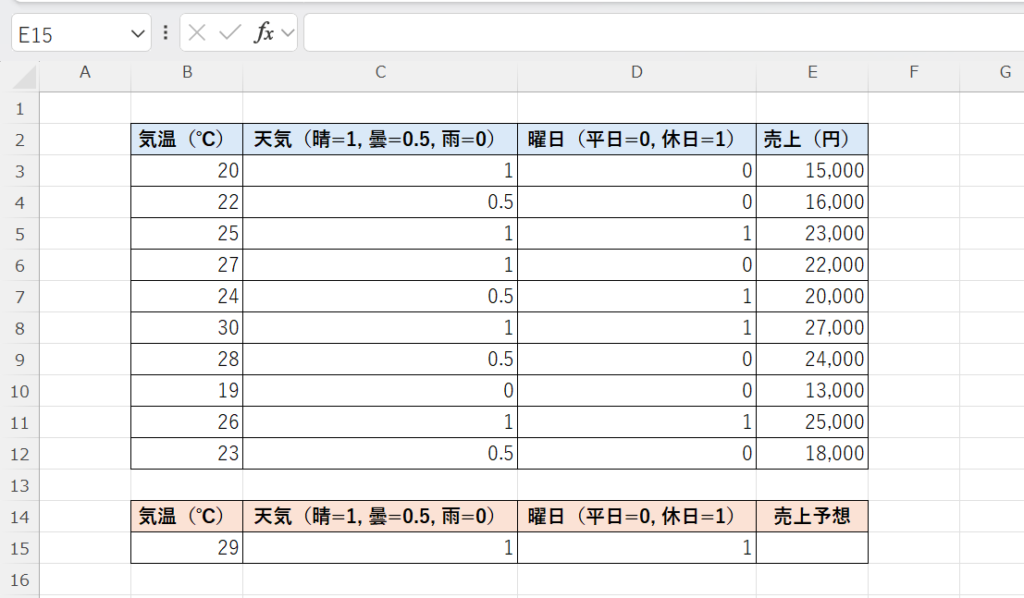
ここでは、気温(℃)・天気(晴/曇/雨)・曜日(平日/休日) の3つの要因を使って、
「気温29℃、晴、休日」のアイスクリームの売上予想をTREND関数によって求めてみましょう。
セルE15に次の式を入力します。
=TREND(E3:E12, B3:D12, B15:D15)
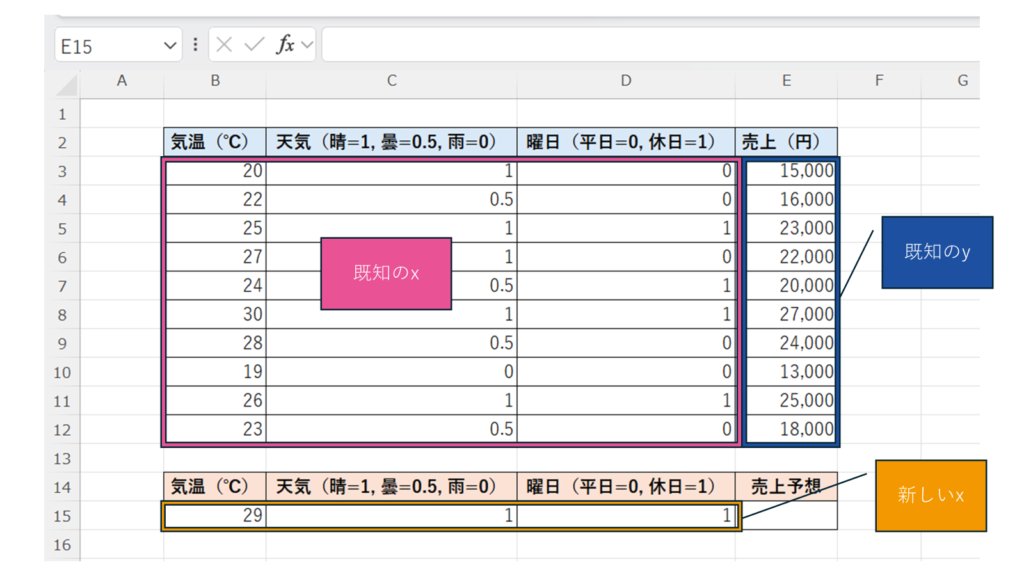
この式では、
- 既知のy:売上データ(目的変数Y)
- 既知のx:気温・天気・曜日の3つの説明変数X
- 新しいx:予測したい新しい条件(気温29℃、晴、休日)
を指定しています。
TREND関数は、この3つの要因を使って重回帰分析を行い、それぞれの影響度(気温・天気・曜日の重み)を自動で求め、その組み合わせから「予測売上」を算出します。
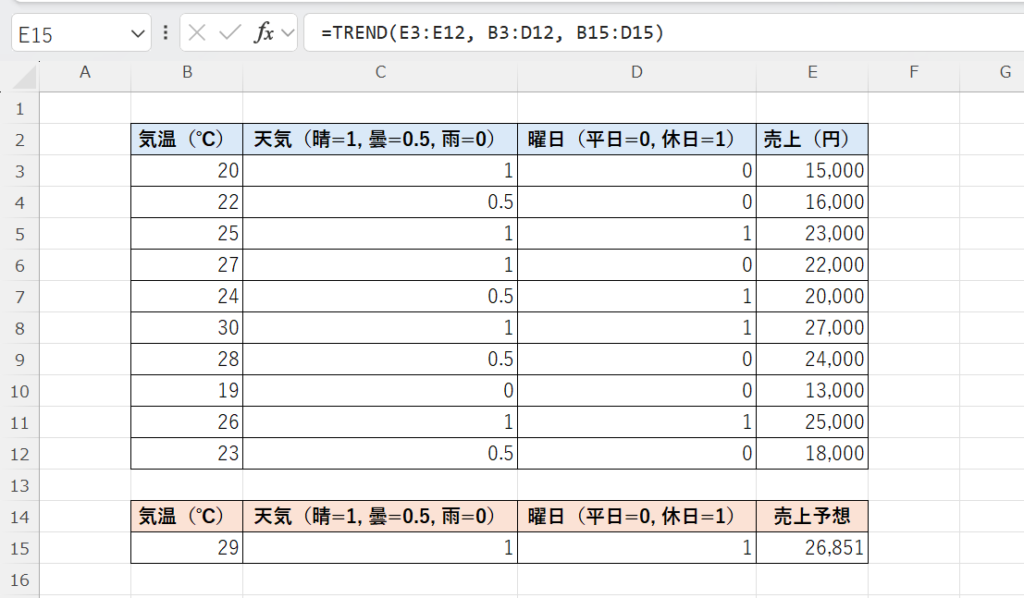
結果は、約26,851円となりました。
つまり、「気温29℃、晴れ、休日」の条件では、売上は約26,851円になると予測できるということです。
活用例
- 売上予測:気温や広告費など複数要因を使った重回帰分析で売上を予測
- 需要分析:気温と販売数量の関係を可視化して在庫計画に活用
- アクセス解析:月ごとのアクセス推移から将来のPVを予測
- マーケティング分析:広告費、来店数、季節要因などを説明変数にした重回帰モデルを作成
注意点
- 直線的な関係(線形関係)の場合に有効
データが大きくばらついている場合や曲線的な傾向には向きません。 - 空白セルや文字列が含まれているとエラーになる
分析の前にデータの整備が必要です。 - 重回帰分析を行う場合は、既知のxを複数列で指定する
例:気温+広告費のように複数要因を指定すると、複数回帰モデルが作れます。
関連関数
| 関数名 | 内容 |
|---|---|
| FORECAST.LINEAR関数 | 単回帰モデルで1つの値を予測 |
| LINEST関数 | 回帰分析の詳細(傾き・切片・決定係数など)を求める |
| GROWTH関数 | 指数関数的な増加を予測(非線形分析) |
| CORREL関数 | 2つの変数の相関関係を求める |
まとめ
TREND関数は、重回帰分析(回帰分析)をExcelで手軽に行える関数です。
過去のデータをもとに将来の値を予測したり、変数間の関係を確認したりすることで、
データに基づく意思決定がしやすくなります。
気温と売上、広告費と来客数など、ビジネスでよく使う関係性を数値で表すのに最適な関数です。
統計ツールを使わなくても、ExcelのTREND関数だけで簡易的な重回帰分析による予測が可能になります。

