平均点が同じでも、「みんな似た点数」なのか「バラバラな点数」なのかで印象は変わりますよね。
この違いを客観的に表してくれるのが 標準偏差 です。データがどれくらい広がっているかを一目でつかめます。
Excelでは、データ全体(母集団)を対象に標準偏差を求めたいときに STDEV.P関数 を使います。
この関数は、旧関数 STDEVP関数 の後継であり、Excel 2010以降では STDEV.P関数 が標準として推奨されています。
STDEV.P関数とは?
STDEV.P関数 は、指定したデータを「母集団(全体)」とみなして、標準偏差 を求める関数です。
標準偏差とは、データの値が平均からどれくらい離れているかを示す指標で、
数値が大きいほどばらつきが大きく、小さいほどデータが平均値の近くに集まっていることを意味します。
標準偏差とは?
標準偏差は、データの「ばらつきの程度」を表す統計指標です。
分散の平方根(√分散)で求められ、元のデータと同じ単位でばらつきを表せるのが特徴です。
たとえば、分散が「107.9」の場合、
標準偏差は √107.9 ≒ 10.4点 になります。
これは、平均値からおおよそ±10点の範囲に多くのデータが分布しているという意味になります。
書式
=STDEV.P(数値1, [数値2], …)
引数の説明
- 数値1, [数値2], …:標準偏差を求めたい数値または範囲。
使用例(テストの点数で母標準偏差を求める)
次の表は、12人のテスト結果です👇
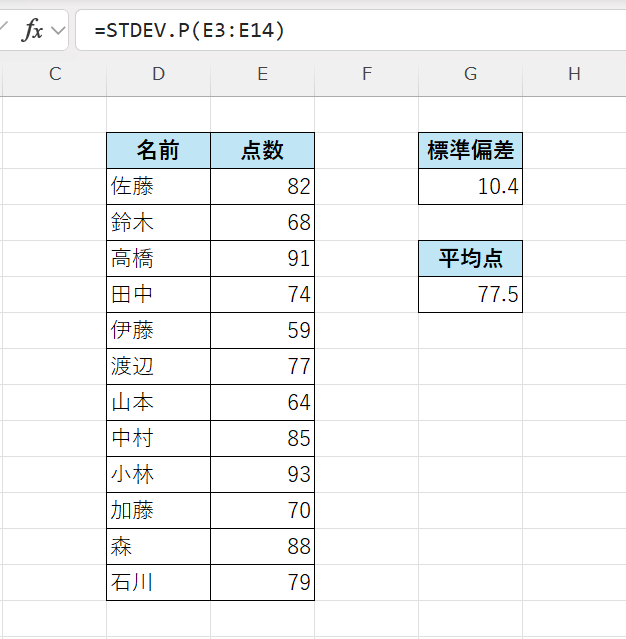
このとき、点数のばらつき(標準偏差)を求めるには次の式を入力します。
=STDEV.P(E3:E14)
👉 結果:およそ 10.4
解説
標準偏差の計算結果「10.4」は、各生徒の点数が平均(約77.5点)からおよそ±10点の範囲に集まっていることを意味します。
この値は、分散(VAR.P)の平方根を取った結果と同じになります。
活用例
- クラスごとのテスト結果の安定性比較
- 製品や機械の測定誤差のばらつきを把握
- 売上やアクセス数など、変動の大きさの分析
- スポーツデータやアンケート結果の信頼性評価
注意点
| 注意点 | 内容 |
|---|---|
| 母集団を対象とする | 全データを含む場合に使用。標本データの場合は STDEV.S を使う。 |
| 小さいほど安定 | 標準偏差が小さいほど、データのばらつきが少ない。 |
| 範囲指定 | 文字列や空白は無視される。 |
| 旧関数との違い | STDEVP は旧関数。現在は STDEV.P を使用。 |
関連関数
| 関数 | 説明 |
|---|---|
| VAR.P | 母分散を求める(STDEV.Pの平方値) |
| VAR.S | 標本分散を求める |
| STDEV.S | 標本標準偏差を求める |
| AVERAGE | 平均値を求める |
まとめ
STDEV.P関数 は、データ全体(母集団)を対象に標準偏差(データのばらつき)を求める関数です。
値が大きいほどデータの散らばりが大きく、小さいほど平均の近くに集中していることを意味します。
テスト結果や売上データなどの「安定性」や「一貫性」を分析する際に、VAR.P(分散)とセットで活用するのがおすすめです。
