PDURATION関数 は、一定の利率で運用した場合に、資金が目標金額に到達するまでの期間を求める関数です。
投資や貯蓄、資産運用の計画を立てる際、「何年で目標金額に到達するのか」を知ることは非常に重要です。
この関数を使えば、複利計算を前提とした期間を簡単に求めることができます。
PDURATION関数とは?
PDURATION関数は、一定の利率で資金を運用した場合に、現在の金額が将来の目標金額に達するまでの期間を求める関数です。
たとえば、100万円を年利5%で運用した場合、200万円になるまでに何年かかるのかを計算できます。
資産形成のシミュレーションや投資計画の立案に役立つ関数です。
書式
PDURATION関数の書式は次のとおりです。
=PDURATION(利率, 現在価値, 将来価値)
引数の説明
- 利率:期間あたりの利率を小数で指定します。(年利5%なら「0.05」と入力)
- 現在価値:現在の金額(元本)を指定します。
- 将来価値:目標とする金額を指定します。
PDURATION関数の使い方
たとえば、100万円を年利5%で運用し、200万円になるまでの期間を求める場合、次のように入力します。
=PDURATION(0.05,1000000,2000000)
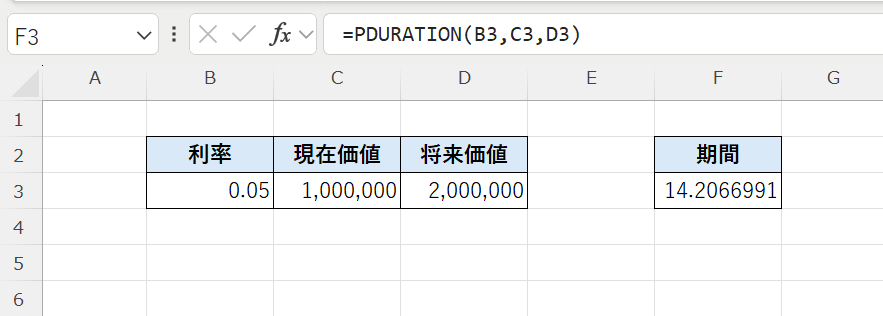
結果は約 14.21 となり、約14.2年で資金が2倍になることを示します。
活用例
PDURATION関数は、資産運用や貯蓄計画を立てる際に非常に役立ちます。
目標金額までの到達期間を把握することで、現実的な資金計画を立てることができます。
また、投資利率ごとに期間を比較することで、利率の違いが長期的にどの程度影響するのかを理解できます。
教育資金や老後資金のシミュレーションにも活用できる実用性の高い関数です。
注意点
PDURATION関数は複利計算を前提とした期間を求めます。
単利計算には対応していません。
利率は必ず小数で入力し、現在価値と将来価値には正の数値を指定する必要があります。
結果は期間(年数)として返されますが、月単位などで考えたい場合は換算が必要です。
関連関数
まとめ
PDURATION関数は、一定の利率で運用した場合に、資金が目標額に到達するまでの期間を求める関数です。
資産形成や投資計画のシミュレーションに役立ち、将来設計を具体的な数値で把握できるようになります。
長期的な資金計画を立てる際に、ぜひ活用したい関数のひとつです。
