Excelで「速度」や「比率」などを平均したいとき、普通のAVERAGE関数では正しい結果が出ないことがあります。
そんなときに使えるのが HARMEAN関数(調和平均) です。
HARMEAN関数を使うと、比率や速度のような「1/x の平均」を求めることができ、実際の平均値をより正確に表せます。
HARMEAN関数とは?
HARMEAN関数 は、指定した数値の 調和平均(ちょうわへいきん) を求める関数です。
調和平均とは、数値の逆数(1/値)の平均を取ったあとに、それを再び逆数にした値のことです。
たとえば「一定距離を異なる速度で移動する場合」や「複数の比率を平均する場合」に適しています。
書式
=HARMEAN(数値1, [数値2], …)
- 数値1, [数値2], …:調和平均を求める値または範囲
使用例
例:速度の平均を求める場合
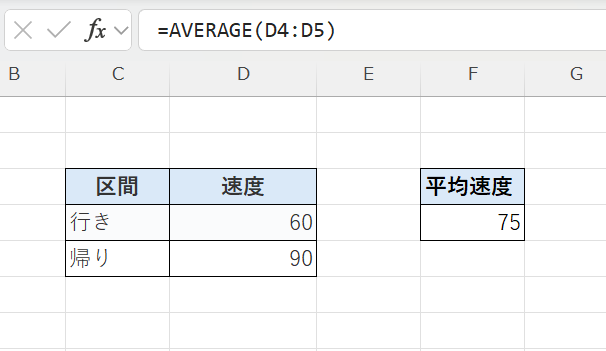
ある車が、同じ距離を「行きは60km/h」「帰りは90km/h」で走ったとします。
| 区間 | 速度(km/h) |
|---|---|
| 行き | 60 |
| 帰り | 90 |
このときの平均速度を単純平均で求めると、(60+90)÷2=75 で「平均速度は75km/h」のように思われますが、これは実際の走行状況を正しく反映していません。
距離が同じで速度が異なる場合、速度の平均を求めるときは、単純に速さの平均を取るのではなく、
全体の距離 ÷ 全体の時間 で求める必要があります。
行きと帰りの距離をそれぞれ180kmとすると、次のように計算できます。
| 区間 | 速度 | 距離 | 時間(距離 ÷ 速度) |
|---|---|---|---|
| 行き | 60km/h | 180km | 180 ÷ 60 = 3時間 |
| 帰り | 90km/h | 180km | 180 ÷ 90 = 2時間 |
合計距離:180 + 180 = 360km
合計時間:3 + 2 = 5時間
したがって、平均速度は次のようになります。
平均速度 = 合計距離 ÷ 合計時間
= 360 ÷ 5
= 72 km/h👉 結果:72 km/h

これは、実際に「60km/hで行き、90km/hで戻ったときの全体の平均速度」が72km/hになることを意味します。
活用例
- 平均速度や平均燃費を求めるとき
- 成長率や変化率の平均を現実的に算出したいとき
- 異なる条件での「単位あたり効率」を平均したい場合
- 複数の投資利回りの平均リターンを求めるとき
注意点
- すべての数値が正である必要がある(0や負の値を含むとエラー)
- 数値の単位を揃えることが重要(km/h、%、倍率など混在禁止)
- AVERAGE関数と同様、空白は無視される
- データの種類に応じて「AVERAGE」「GEOMEAN」「HARMEAN」を使い分けると正確な分析が可能
関連関数
| 関数 | 説明 |
|---|---|
| AVERAGE | 通常の算術平均を求める |
| GEOMEAN | 比率や成長率の平均(幾何平均)を求める |
| MEDIAN | 中央値を求める |
| SUMPRODUCT | 重み付き平均など複雑な平均計算に使える |
まとめ
HARMEAN関数は、「速度」「比率」「効率」など、逆数の関係を持つデータに対して正しい平均を求める関数です。
算術平均(AVERAGE)では誤差が出る場面でも、HARMEANを使えば実際の平均効果を正しく表現できます。
GEOMEANとあわせて覚えておくと、より高度なデータ分析ができるようになります。
