「気温が上がるとアイスクリームの売上が増える」――
このように、2つのデータの間にどのくらい関係性があるかを
調べたいときに使えるのが CORREL関数 です。
CORREL関数を使えば、
「どの程度、2つのデータが一緒に増減しているか(=相関関係)」を数値で確認できます。統計分析やデータ傾向の確認にとても役立つ関数です。
CORREL関数とは?
CORREL関数 は、2つのデータ範囲の間にある「相関係数」を求める関数です。
相関係数は −1~1 の範囲で表され、次のような意味を持ちます。
| 値の範囲 | 意味 |
|---|---|
| 1 に近い | 強い正の相関(片方が増えるともう一方も増える) |
| 0 に近い | 相関なし(関係がほとんどない) |
| −1 に近い | 強い負の相関(片方が増えるともう一方は減る) |
書式
=CORREL(配列1, 配列2)
引数の説明
- 配列1:相関を調べたい1つ目のデータ範囲
- 配列2:相関を調べたい2つ目のデータ範囲
使用例
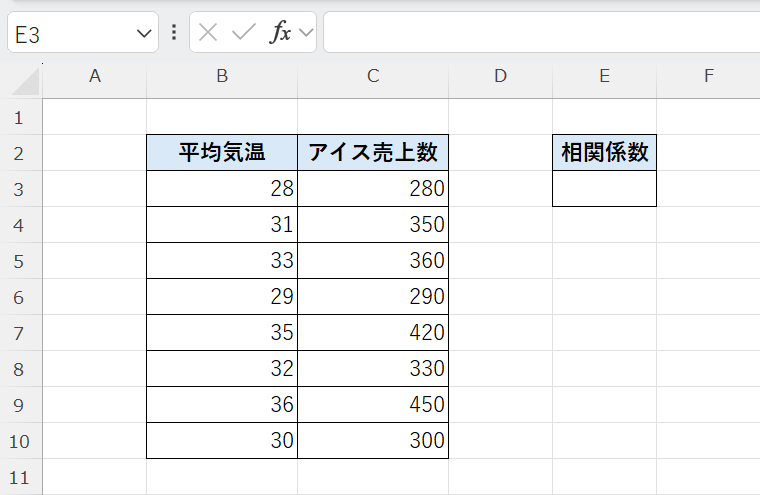
例:気温とアイスクリームの売上の関係を調べる
ここでは、気温とアイスクリームの売上データを用意し、
両者の間にどの程度の相関関係があるのかを、CORREL関数を使って確認します。
=CORREL(B3:B10,C3:C10)
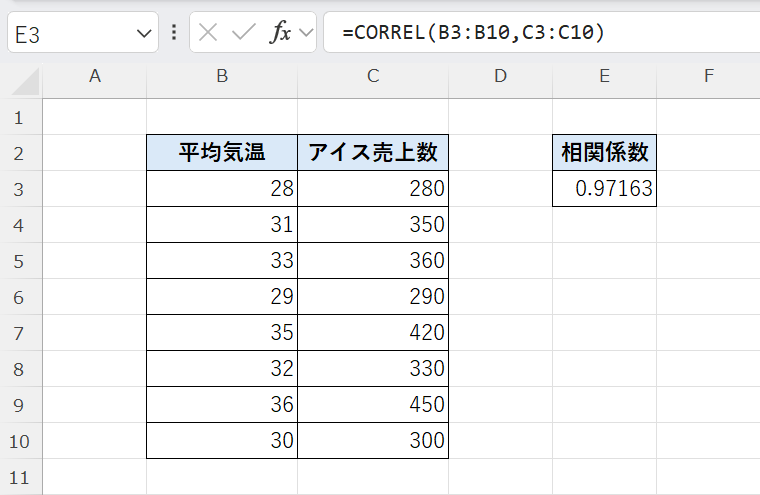
CORREL関数で計算した結果、相関係数は 0.97163(約0.97) でした。
これは非常に高い値で、気温が上がるほどアイスクリームの売上も増える強い正の相関関係があることを示しています。
「暑い日はアイスがよく売れる」という傾向がデータ上でもはっきり確認できる結果です。
相関係数の目安(一般的な基準)
| 相関係数の範囲 | 相関の強さ |
|---|---|
| ±0.00〜±0.19 | ほぼなし |
| ±0.20〜±0.39 | 弱い相関 |
| ±0.40〜±0.59 | 中程度の相関 |
| ±0.60〜±0.79 | 強い相関 |
| ±0.80〜±1.00 | 非常に強い相関 |
今回の相関係数(0.97)は「非常に強い正の相関」に該当します。
実際の生活でも、暑い日ほどアイスクリームを食べたくなりますが、
この相関係数(0.97) は、その関係をほぼ完全に数値化していると言えます。
活用例:データ分析や傾向確認に使える
CORREL関数は、次のような場面で活用できます。
- 気温と飲料・アイスの売上関係を分析
- 勉強時間とテストの得点の関係を調べる
- 広告費と売上金額の関係を分析
- アクセス数と収益の関係を確認
「どちらかの値が増えると、もう一方がどう変化しているか」を
シンプルに可視化できるのが最大の強みです。
注意点
- データの個数が一致していない場合はエラーになります。
- 空白や文字データが含まれていると、正しい結果が出ません。
- 外れ値(極端な値)があると相関係数が歪むことがあります。
関連関数
| PEARSON関数 | CORRELと同じく相関係数を求める関数 |
| COVARIANCE.P関数 | 共分散を求める(相関関係のもとになる数値) |
| FORECAST関数 | 相関を利用して将来の値を予測する |
まとめ
CORREL関数は、2つのデータの間に「どの程度の関係性があるか」を数値で示す関数です。結果が1に近いほど強い正の相関、−1に近いほど強い負の相関を意味します。
「データ同士の関係をざっくり把握したい」ときに、まず使ってみると分析の出発点になります。

