住宅ローンやカードローンなどを返済しているとき、毎月の支払額の中で、元金相当分がいくらなのか気になることがありますよね。そんなときに役立つのが PPMT関数 です。
PMT関数が「毎月の返済額(元金+利息)」を求めるのに対し、PPMT関数はそのうちの元金部分だけを計算できます。
ローンの返済計画や、残高シミュレーションを行いたいときに便利な関数です。
PPMT関数とは?
PPMT関数(Principal Payment) は、指定した支払い期間における元金の返済額を求める関数です。
ローンや借入のように「定期的に支払いを行う場合」に使われ、
返済額のうち「どれだけ元金が減っているか」を知ることができます。
書式
=PPMT(利率, 期, 期間, 現在価値, [将来価値], [支払期日])
引数の説明
- 利率:1回あたりの利率
- 期:どの支払い回(期)を求めるか(例:1=1回目、12=12回目)
- 期間:支払い回数
- 現在価値:借入金額
- [将来価値](省略可):借入金を完済する場合は0を指定。
- [支払期日](省略可):支払いタイミング。0=期末払い、1=期首払い(省略時は0)。
※毎月の返済額を求める場合、利率は年利÷12で月利を求める。期間も同様に年数×12で月数を求める。
使用例
例:利率15%、借入金10万円を1年で返すカードローンの元金部分を求める
条件
- 借入金:100,000円
- 期間:1年(12か月)
- 年利:15%(月利=15%÷12)
1回目の支払い(期間=1)の元金部分を求めるには👇
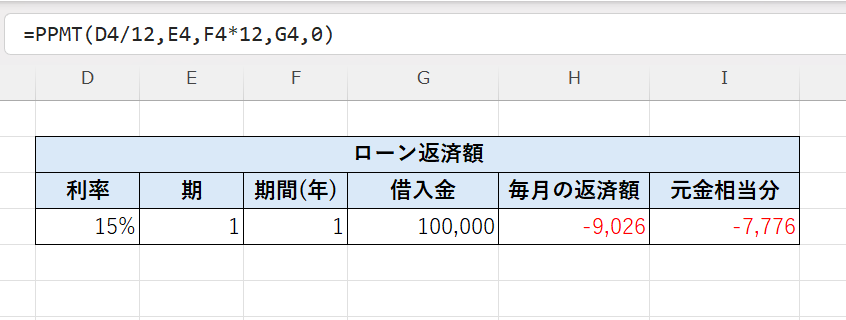
👉 結果:7,776円(1回目の元金返済分)
同じ条件で、
2回目(期間=2)の場合は👇
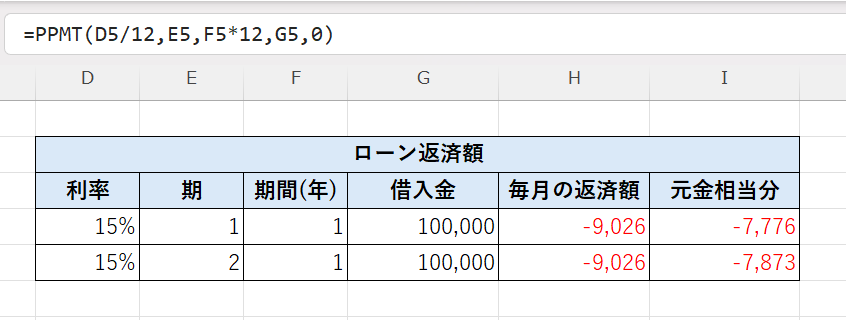
👉 結果:7,873円(2回目の元金返済分)
このように、回数を重ねるごとに利息が減り、元金の返済額が少しずつ増えていきます。
💡 PMT関数との違い
| 関数 | 求められる内容 | 例 |
|---|---|---|
| PMT | 毎回の支払総額(元金+利息) | 約9,026円 |
| PPMT | そのうちの元金部分 | 約8,776円(初回) |
| IPMT | そのうちの利息部分 | 約250円(初回) |
活用例
- ローンの返済スケジュールを作成(回数ごとの元金と利息を分ける)
- 年間の返済予定表を作る
- 家計簿で「返済のうち利息分はいくらか」を把握する
- 返済初期と後半の支払い構造を比較して可視化
注意点
| 注意点 | 内容 |
|---|---|
| 利率は「1回あたり」に換算する | 年利をそのまま入れると結果が誤る(÷12などにする) |
| 結果がマイナスになる | 支払い(出費)を意味するため。-PPMT() とすれば正の値で表示可能 |
| 期間の指定に注意 | 1回目=1、12回目=12のように整数で指定する |
| PMT・IPMTと組み合わせると便利 | 総額・利息・元金の内訳を一括計算できる |
関連関数
| 関数 | 説明 |
|---|---|
| PMT | 毎回の支払総額(元金+利息)を求める |
| IPMT | 利息部分の支払額を求める |
| PV | 現在価値(借入金の元金)を求める |
| NPER | 支払回数を求める |
まとめ
PPMT関数は、ローンや借入の返済額のうち「元金にあたる部分だけを算出」できる関数です。
PMT関数と組み合わせれば、返済額の内訳(元金と利息)を明確に把握できます。
ローン返済表や家計シミュレーションを作る際に、ぜひ活用してみましょう。
