Excelで平均を求めるとき、多くの人が使うのは AVERAGE関数(算術平均) ですが、
データの性質によっては GEOMEAN関数 (幾何平均) のほうが適切な場合があります。
「成長率」「変化率」「比率」などを扱うときは、幾何平均を使うことでより正確な傾向を把握できます。この記事では、GEOMEAN関数の使い方をわかりやすく解説します。
GEOMEAN関数とは?
GEOMEAN関数 は、指定した数値の 幾何平均(きかへいきん) を求める関数です。
幾何平均とは、複数の数値をすべて掛け合わせて、その積の n 乗根(n は数値の個数)を取った平均のことです。
数値の増減や割合(率)を扱うときに使われ、平均的な伸び率や成長率 を求めるのに適しています。
書式
=GEOMEAN(数値1, [数値2], …)
| 引数 | 説明 |
|---|---|
| 数値1 | 幾何平均を求める1つ目の値または範囲 |
| [数値2], … | 追加の数値または範囲(最大255個まで指定可能) |
使用例
たとえば、ある商品の売上が2年間で
「1年目:2倍 → 2年目:0.5倍」と変化したとします。
AVERAGE関数を使って平均を求めると次のようになります。
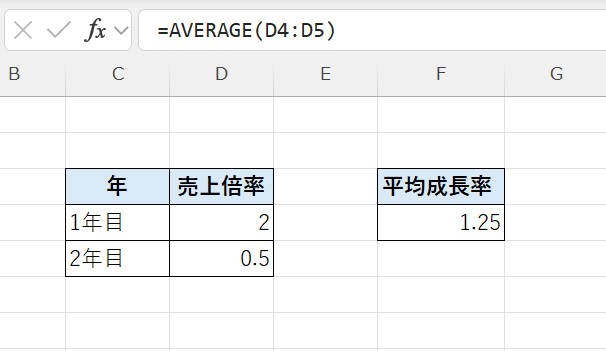
一見「平均で1.25倍(25%増)」のように見えますが、
実際には 2倍になったあと0.5倍に下がっている ため、最終的な売上は「元の水準と同じ(1倍)」に戻っています。つまり、1.25倍という結果は現実を反映していません。
一方、幾何平均を使うと「実際にどれくらい平均的に伸びたのか」を正しく表せます。
同じデータを GEOMEAN関数 で計算します。
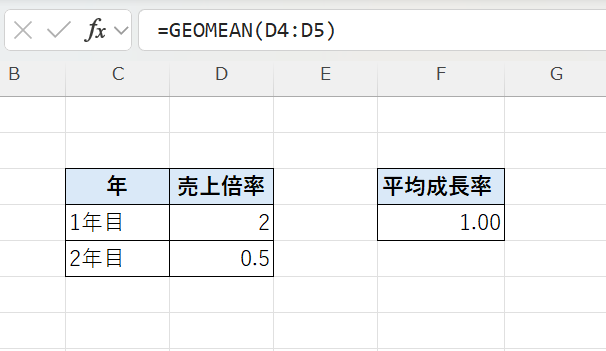
GEOMEAN関数で計算した結果、平均成長率は等倍(1倍) となります。
これは実際の結果(増減が打ち消し合って元に戻る)を正しく表しています。
💡この例から分かるように、幾何平均(GEOMEAN)は「成長率」「変化率」「複利」のような掛け算で変化するデータに最適です。
単純平均では見落とされる“実際の増減のバランス”を正しく表現できます。
活用例
- 投資や株価の 平均成長率(CAGR) を求める
- 売上やアクセス数などの 前年比伸び率 の平均を分析
- 成長率・比率データのブレを小さくして傾向を把握
- 複数商品の価格変動を一括比較する場合にも有効
注意点
- 0または負の値を含むとエラーになる(幾何平均は正の値でのみ計算可能)
- 欠損値や空白は無視される
- 単位が「比率(例:1.05=5%増)」であることを確認して使う
- 負のデータや0を扱いたい場合は、
LOG関数やEXP関数との組み合わせが必要
関連関数
| 関数 | 説明 |
|---|---|
| AVERAGE | 通常の算術平均を求める |
| HARMEAN | 調和平均を求める(速度や比率の平均に使用) |
| MEDIAN | データの中央値を求める |
| POWER | べき乗計算により幾何平均を手動で計算できる |
まとめ
GEOMEAN関数は、比率や成長率などの「掛け算で変化するデータ」の平均を求めるときに使う関数です。
通常の平均(AVERAGE)よりも現実的な結果が得られるため、投資分析や業績比較などで重宝します。
AVERAGE・HARMEANなどとあわせて覚えておくと、データの性質に応じた正しい平均値を使い分けられます。
