「気温が下がるほど暖房の使用量が増える」――
このように、2つのデータの間にどのような関係があるのかを
確認したいときに便利なのが PEARSON関数 です。
PEARSON関数は、2つの数値データの間にどれくらいの「相関関係」があるかを調べ、
その強さを −1~1の数値(相関係数) で示します。
PEARSON関数とは?
PEARSON関数 は、2つの数値データの間にある「ピアソンの積率相関係数」を求める関数です。
Excelの CORREL関数 とほぼ同じ働きをします。
| 相関係数の値 | 意味 |
|---|---|
| 1 に近い | 強い正の相関(片方が増えるともう一方も増える) |
| 0 に近い | 相関なし(関係がほとんどない) |
| −1 に近い | 強い負の相関(片方が増えるともう一方が減る) |
書式
=PEARSON(配列1, 配列2)
引数の説明
- 配列1:相関を求めたい1つ目のデータ範囲
- 配列2:相関を求めたい2つ目のデータ範囲
使用例
例:外気温と暖房使用量の関係を調べる
ここでは、外気温(℃)と暖房使用量(kWh)のデータを使って、
両者の間にどの程度の相関関係があるのかを PEARSON関数 で分析します。
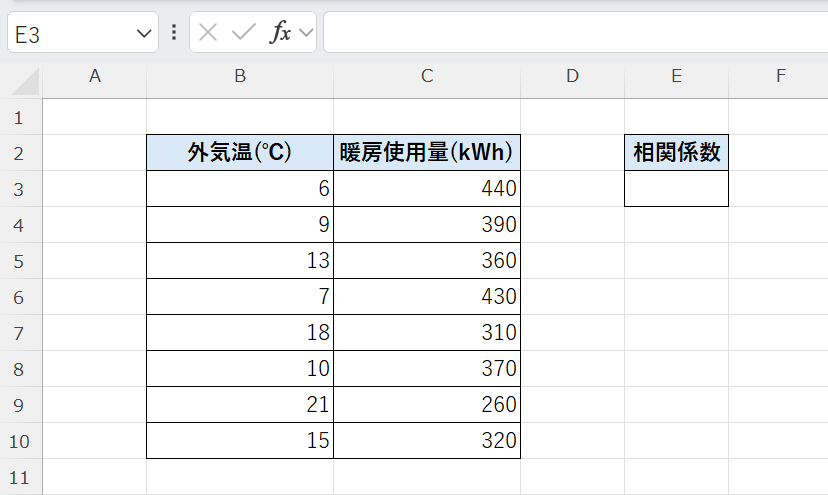
=PEARSON(B3:B10,C3:C10)
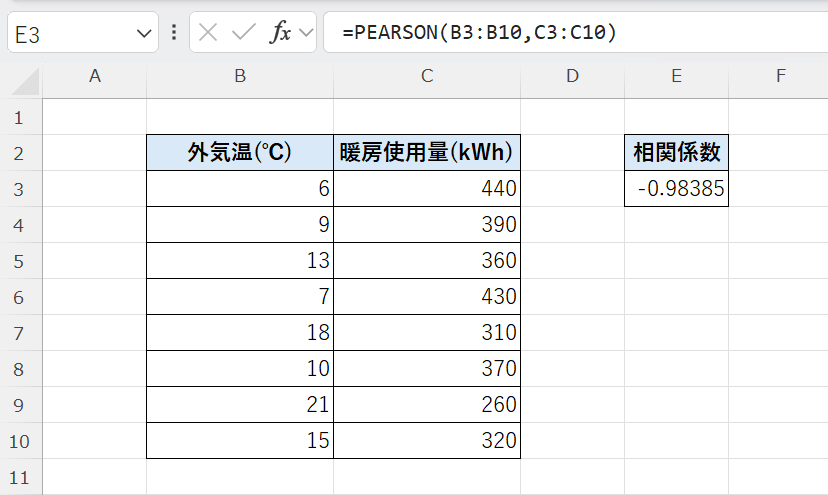
PEARSON関数で計算した結果、相関係数は −0.98385 となりました。
この値は −1 に非常に近いため、外気温と暖房使用量の間には非常に強い負の相関関係があるといえます。
つまり、気温が下がるほど暖房の使用量が増え、気温が上がるほど使用量が減る という関係が、データ上でもはっきりと確認できる結果です。
相関係数の目安(一般的な基準)
| 相関係数の範囲 | 相関の強さ |
|---|---|
| ±0.00〜±0.19 | ほぼなし |
| ±0.20〜±0.39 | 弱い相関 |
| ±0.40〜±0.59 | 中程度の相関 |
| ±0.60〜±0.79 | 強い相関 |
| ±0.80〜±1.00 | 非常に強い相関 |
今回の例(−0.98)は「非常に強い負の相関」に該当します。
実際の生活でも、寒い日ほど暖房を多く使う傾向がありますが、
この相関係数の値(−0.98)はその傾向をほぼ完全に数値化しているといえます。
注意点
- データ数が一致していないとエラー(#N/A)になります。
- 空白や文字データを含むと正しく計算できません。
- 外れ値(極端な値)があると結果が大きく歪むことがあります。
関連関数
| CORREL関数 | 相関係数を求める。PEARSONと結果は同一。 |
| COVARIANCE.P関数 | 共分散を求める。相関係数のもとになる値。 |
| FORECAST.LINEAR関数 | 相関をもとに将来値を予測する。 |
まとめ
PEARSON関数は、2つのデータの関係性を数値で示す統計関数です。
今回の例のように「気温が下がると暖房使用量が増える」といった相関関係を確認するのに最適です。
相関係数を求めることで、
「感覚的な関係」をデータで裏付けることができるのが大きなメリットです。

