毎月の貯金や定期積立を続けると、最終的にどれくらいのお金になるのか気になりますよね。
Excelの FV関数 を使えば、一定の金額を継続的に積み立てた場合の将来の合計金額(将来価値) を簡単に計算できます。
FV関数とは?
FV関数(フューチャーバリュー) は、
「毎回一定の金額を積み立てたとき、将来いくらになるか」を求める関数です。
金利(利息)を考慮して、最終的な資産の金額を自動計算できます。
書式
=FV(利率, 期間, 定期支払額, 現在価値, 支払期日)
引数の説明
- 利率:利率を指定します。
年利3%なら「3%/12」で月利に変換します。 - 期間:積立を行う回数です。
10年間毎月なら10*12(=120回)。 - 定期支払額:毎回積み立てる金額を指定します。
- 現在価値:すでにある元本がある場合に指定します。
積立だけの場合は0。 - 支払期日:支払いタイミングを指定します。
0 = 期末払い(通常)/ 1 = 期首払い。
使用例
毎月5万円を10年間、年利3%で積み立てた場合の将来金額を求める
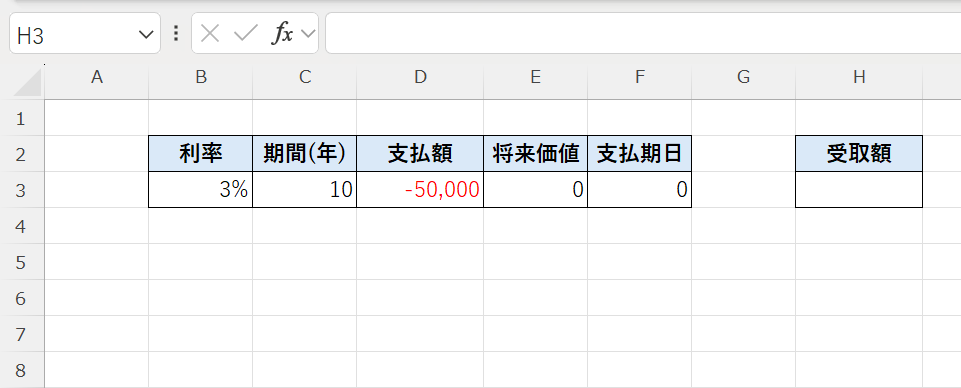
毎月5万円を10年間、年利3%(月利0.25%)で積み立てた場合をFV関数で計算すると、次のようになります。
=FV(B3/12,C3*12,D3,E3,F3)
- 利率:年利3%で毎月積み立ての場合 →
- 期間:10年間毎月なら 10*12(=120回)
- 支払額:積立金は支出なので「-50000」とマイナスで入力します。
- 現在価値:今回のように「ゼロから積立」なら 0。
- 支払期日:0=期末払い(通常)/1=期首払い。
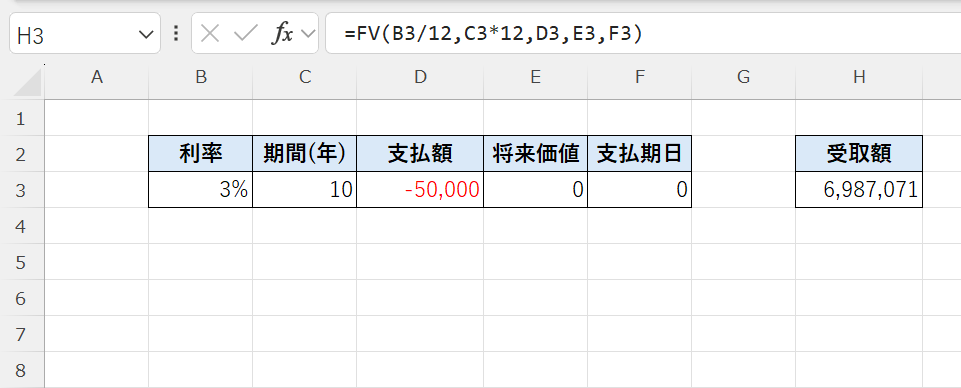
結果は 約6,987,071円(約699万円) です。
毎月5万円を10年間積み立てると、元本は600万円になりますが、年利3%で運用すると利息の効果によって約99万円増え、最終的に約6,987,071円まで成長します。
このように、少しの金利でも長期間続けることで「複利(利息が利息を生む)」の効果が積み重なり、着実にお金を増やすことができます。
活用例
FV関数は、次のようなシミュレーションに便利です。
- 毎月の定期預金・つみたて投資の将来金額
- 教育資金や住宅資金の目標額のシミュレーション
- 老後の積立プランを検討するときの資産予測
注意点
- 支払額(積立額)はマイナスで入力しないと、結果がマイナスになります。
- 金利は「1回あたり」で指定する必要があります(年利の場合は÷12)。
- 金利が0の場合でも使えますが、単純な積立金額の合計になります。
関連関数
まとめ
FV関数を使えば、積立や貯蓄が将来いくらになるかを簡単に試算できます。
金利や期間、積立額を少し変えるだけで、将来の資産計画を具体的にシミュレーションできる便利な関数です。

